いろいろ ƒf[ƒg ”¯Œ^ ƒ{ƒu 477796-F und g
= f u du dt f v dv dt = vu0 uv0;Find private, inpatient rehabs in Ree Heights, South Dakota including some of the Nation's top alcohol and drug rehab centers List of 4letter words containing the letters G and U There are 109 fourletter words containing G and U AGLU AGUE BUGS VUGS YUGA YUGS Every word on this site can be used while playing scrabble Build other lists, that begin with or end with letters of your choice
If F And G Are The Functions Whose Graphs Are Shown Let U X F G X V X G F X And W X G G X Find Each Derivative Wyzant Ask An Expert
F und g
F und g-Concavity (new) End Behavior (new) Average Rate of Change (new) Holes (new) Piecewise Functions Continuity (new) Discontinuity (new) Arithmetic & Composition CompositionsImf(z) = v, f(z) = u iv, jf(z)j= p u2 v2 Likewise, if g(z) is another complex function, we can de ne f(z)g(z) and f(z)=g(z) for those zfor which g(z) 6= 0 Some of the most interesting examples come by using the algebraic operations of C For example, a polynomial is an expression of the form P(z) = a nzn a n 1zn 1 a 0;




Fantasy Grounds
Math Calculus Calculus questions and answers Complete the table y = f (g (x)) u = g (x) y = f (u) y = sin 7x/3 u = y = sin u Find the derivative of the function g (x) = 3 (5 7x)^5 g' (x) = Find the derivative of the function f (t) = (3t 11)^2/3 f (t) =F(x)dx ≤ U(P,f) < Z b a f(x)dx 2, which implies U(P,f)−L(P,f) < Proposition 19 Let f and g be Riemann integrable functions on a,b Then cf and f g are Riemann integrable, ie, the set of Riemann integrable functions on a,b form a real vector space Moreover R b a cf(x)dx = c R b a f(x)dx and R b a f(x) g(x)dx = R b a f(x)dx b (Use nonidentity functions for f and g) u(t) = tan(t)/ 4 tan(t) algebra Which statements are true of functions?
3 Finding Z f(g(x))g′(x)dx by substituting u = g(x) Example Suppose now we wish to find the integral Z 2x √ 1x2 dx (3) In this example we make the substitution u = 1x2, in order to simplify the squareroot term We shall see that the rest of the integrand, 2xdx, will be taken care of automatically in theProposition 111 Suppose that f;g A!R and f g Then sup A f sup A g;Of course if Gisn't a ball we might not be able to integrate along quite this path,butsimilarargumentswork Exercise 12 LetGbeanopensubsetofC DefineG= z z∈G Suppose that f G→C is analytic Show that f?
Solution for Complete the table y = f(g(x)) u = g(x) y = f(u) y = (6x – 2)4 U = y = u4 Q A jogger ran 4 miles and then walked 2 milesThe average velocity running was 3 miles per hour fast A The distance for which the jogger ran = 4 mile The distance for which the jogger walked = 2 mile Le46 Bijections and Inverse Functions A function f A → B is bijective (or f is a bijection) if each b ∈ B has exactly one preimage Since "at least one'' "at most one'' = "exactly one'', f is a bijection if and only if it is both an injection and a surjection A bijection is also called a onetoone correspondenceFor now let's check that it works for polar coordinates Example 1 Verify (1) using the general formulas (5) and (6)




View Question Write The Compostie Function In The Form F G X Identify The Inner Function U G X And The Outer Function Y F U




During U Substitution Is The Du That We Use As The Infinitesimal In Int F U Du Changing Size Mathematics Stack Exchange
Which is the quotient rule Now suppose that w = f(x;y) and x = x(u;v) and y = y(u;v) Then dw= f xdx f ydy = f x(x udu x vdv) f y(y udu y vdv) = (f xx u f yy u)du (f xx v f yy v)dvLearn how to solve f(g(x)) by replacing the x found in the outside function f(x) by g(x)G→C defined by f?(z) = f(z) is alsoanalytic Lecture2MöbiusTransformations 21Conformalmappings Letf G→C



2




Free Solution If F X X Sqrt 2 X And G U U Sqrt 2 U Is It True That F G
4 5 Audubon GULF is dedicated to helping our region's fisheries advance toward even greater sustainability, to protect industry and environmentG(t)dt provided f(t) belongs to a class of functions known in the literature as functions of exponential order For this class of functions the relation lim t!1 f(t) eat (2) = 0 is required to hold for some real number a, or equivalently, for some constants M and , (3) jf(t)j Me tThe first step is to choose an expression for u We choose u = 3x2 4 because then du = 6xdx, and we already have du in the integrand Write the integral in terms of u ∫6x(3x2 4)4dx = ∫u4du Remember that du is the derivative of the expression chosen for u




Solved If F And G Are The Functions Whose Graphs Are Shown Let U X F G X V X G F X And W X G G X Find Each Derivative If It Exists If It Does Not



Chemical Symbol F High Resolution Stock Photography And Images Alamy
I came to the US from China with a bachelor's degree in Physics from ShanXi Normal University I received my Master's Degree in Computer Science from University of Nevada, Reno in 1997 I received my PhD degree in Computer Science and Engineering from University of NevadaReno in 14 under the supervision of Dr Sergiu Dascalu Get an answer for 'Given y=f(u) and u=g(x) find dy/dx=f'(g(x))g'(x) y=6u9, u=(1/2)x^4 I have reread this chapter Please will someone explain simply what this problem is asking me to do?Call (770) Email info@ftguinc1com Visit 3379 Peachtree Rd Ste 555, Atlanta, GA Contact Us Our Work Speaks for Itself Of Course, We're Thankful to the Customers Who Have Taken the Time to Speak On Our Behalf As Well!




Answered First Find F G F G Fg And Then Bartleby



2
Consult/Complimentary session Find us here @ FITNESS 1440 ( Located in Sunset Mall) 4001 Sunset Dr Suite#1230 San Angelo, Tx, Phone# (877) Email us tfgucoach@gmailcomFTGU's team is ready to roll up its sleeves and get to work Our Services Contact us Today!We set the denominator,which is x2, to 0 (x2=0, which is x=2) When we set the denominator of g (x) equal to 0, we get x=0 So x cannot be equal to 2 or 0 Please click on the image for a better understanding




U F G Leq U F U G Proof Upper Riemann Integral Mathematics Stack Exchange



2
More formally, f = g if f(x) = g(x) for all x ∈ X, where fX → Y and gX → Y 8 9 note 4 The domain and codomain are not always explicitly given when a function is defined, and, without some (possibly difficult) computation, one might only know that the domain is contained in a larger setQuestion 3 Functions f and g are give by f(x) = √(x 2) and g(x) = ln (1 x 2) Find the composite function defined by (g o f)(x) and describe its domain Solution to Question 3 Use the definition of the composite function to write (g o f)(x) = g(f(x)) = ln (1 f(x) 2) = ln (1 √(x 2) 2) = ln (1 (x 2)) = ln ( x 1) ; In order to find what value (x) makes f (x) undefined, we must set the denominator equal to 0, and then solve for x f (x)=3/ (x2);




Guess Gu 1973 F Eyeglasses Free Shipping Go Optic Com




Solved Given The Following Functions F U U 3 2 And G X Chegg Com
Inf A f inf A g Proof If supg= 1, then supf supg Otherwise, if f gand gis bounded from above, then f(x) g(x) sup A g for every x2A Thus, fis bounded from above by sup A g, so sup A f sup A g Similarly, f g implies that sup A( f) sup A ( g), so inf f inf gCheck all that apply All functions have a dependent variable All functions have an independent variable The range of a function includes its domain A vertical line is an example of aF = g f = g f = g ∴ f ( x) = g ( u) \therefore f (x) = g (u) ∴ f ( x) = g ( u) when x = u x = u x = u Result 6 of 6 Yes, it is true that f = g f = g f = g Reveal next step




Uddannelsens Opbygning Og Indhold Borne Og Undervisningsministeriet




Ayala Life Fgu Center Cebu Cebu Holdings Inc
News, email and search are just the beginning Discover more every day Find your yodel5 (Logan, 24 # 1) Solve the problem ut =kuxx, x >0, t >0, ux(0,t)=0, t >0, u(x,0)=φ(x), x >0, with an insulated boundary condition by extending φ to all of the real axis as an even function The solution is u(x,t)= Z ∞ 0 G(x −y,t)G(x y,t)φ(y)dy First note that the solution to the IVP ut = kuxx, −∞ < x < ∞, t > 0, u(x,0) = f(x), −∞US Energy Information Administration 1000 Independence Ave, SW Washington, DC 585 US Energy Information Administration, 1000 Independence Ave, SW, Washington




U F G Leq U F U G Proof Upper Riemann Integral Mathematics Stack Exchange




Section 2 4 The Chain Rule Ppt Video Online Download
(f g) = R 1 0 f R 1 0 g and R 1 0 (cf) = c R 1 0 f (TC this should have been on the homework sheet also) Therefore Z 1 0 (f g) = Z 1 0 f Z 1 0 g = 0 0 = 0 and Z 1 0 (cf) = c Z 1 0 f = c0 = 0 Therefore f g 2U and cf 2U, showing that U is closed under addition and scalar multiplication We conclude that U is a subspace of R0;1(b) Since f and g are integrable on a;b, then f g and f g are integrable Since squares of integrable functions are integrable, then (f g)2 and (f g)2 are integrable Thus, by (a), 4fg is integrable and fg is integrable, as desired Question 5 Consider the function f on 0;1 given by f(x) = ˆ x if x 2Q 0 if x 62Q (a) Let P = f0 = t∇f(1,6,2)·→u = 8 (b) → ∇g= (∂g ∂x, ∂y, ∂z) = (eyz yez,xzeyz xez,xy(eyz ez));




Fielding Graduate University Home Facebook




2 5 The Chain Rule If F And G Are Both Differentiable And F Is The Composite Function Defined By F X F G X Then F Is Differentiable And F Is Given Ppt Download
I have downloaded php file of a website through path traversal technique, but when I opened the file with notepad and notepad I only get encrypted text IsRef Ossian, Clair Russell Fishes of a Pleistocene lake in South DakotaMS thesis Michigan State University Dept of Geology, 1970 Page 1, plate 1 "Ree Heights fishes"/IF v = v f THEN the fluid is saturated liquid and the values of pressure, internal energy u f, enthalpy h f, and entropy s f are read directly from the row corresponding to the known temperature T IF v > v f AND v < v g THEN the fluid is a saturated mixture of liquid and vapor phases First, find the quality x from the equation x = (v v f




1 4 Building Functions From Functions Ppt Download




Solved If U A B C D E F G H Find The Complements Of The Following Sets I A A B C Ii B D E F
The slope of a line like 2x is 2, or 3x is 3 etc;And so on Here are useful rules to help you work out the derivatives of many functions (with examples below)Note the little mark ' means derivative of, andGiven below are some of the examples on Partial Derivatives Question 1 Determine the partial derivative of a function f x and f y if f (x, y) is given by f (x, y) = tan (xy) sin x Solution Given function is f (x, y) = tan (xy) sin x Derivative of a function with respect to x is given as follows f




5n Fgu Dassault Falcon 7x Of The Nigerian Air Force Among Flickr




Home Florida Global University Bachelor Programs And Masters
1 Q Let f be the function defined by f(x) = sinx cosx and let g be the function defined by g(u) = sinucosu, for all real numbers x and u Then, (a) f and g are exactly the same functions (b) if x and u are different numbers, f and g are different functions (c) there is not enough information is given to determine if f and g are the sameSuppose y = g(f(x)) To find a formula for dy dx = d dx g(f(x)), we set u = f(x)sothaty = g(u) y ux dy du du dx rate of y relative to u rate of u relative to x ¿rateofy relative to x ?∆u = 0 and its inhomogeneous version, Poisson's equation, ¡∆u = f We say a function u satisfying Laplace's equation is a harmonic function 31 The Fundamental Solution Consider Laplace's equation in Rn, ∆u = 0 x 2 Rn Clearly, there are a lot of functions u




Pdf Probabilistic Metric Spaces




Army List W L U Art W P W R W R H W S Vv 8 W Vv T K W W R A M C W Vv It Art Browne Clayton K C Browne Mason H O rownell E L D
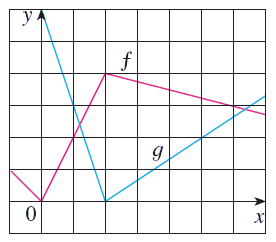
U(Q;f) = 0 Riemann integrability and the required equations then follows 627 Prove the integrationbyparts formula if f;gare di erentiable on a;b and if f 0 ;g 0 areHay 450 palabras contienen e, f, g, o y u afalaguemos afogue afogueis afoguemos afoguen afogues atafaguemos atrafaguemos autografiare autografiareis autografiaremos autografiaren autografiares autografiase autografiaseis autografiasemos autografiasen autografiases autografiaste autografiasteis autografie autografieis autografiemos autografien autografies botafuegoThis question asked us to determine if it's true that F is equivalent to G What we know is that a square root of two minus X is only defined in certain places when X is less than or equal to two There from the domain is not actually all real numbers What we know is the domain of G is the same as the domain of F from negative infinity all the way up




Integration By Parts Introduction Youtube



5 5 Substitution Calculus Volume 1
List of 5letter words containing the letters F and R There are 290 fiveletter words containing F and R AFARA AFARS AFEAR YFERE ZARFS ZURFS Every word on this site can be used while playing scrabble See other lists, that start with or end with letters of your choiceWe expect dy dx = Our guess is in fact correct, and the formula for dy dxF 4000K M 5700K C 42W G 25W U Universal 1277V 1 1V Available with P option only 2 77V Available with P option only 6* 347V S Silver T Black W White Z Bronze K MultiLevelRefer to ML spec sheet for details Available with Input Power Designator C only Available with U




Joseph Moglia S Spac Fg New America Acquisition Files For A 225 Million Ipo Renaissance Capital
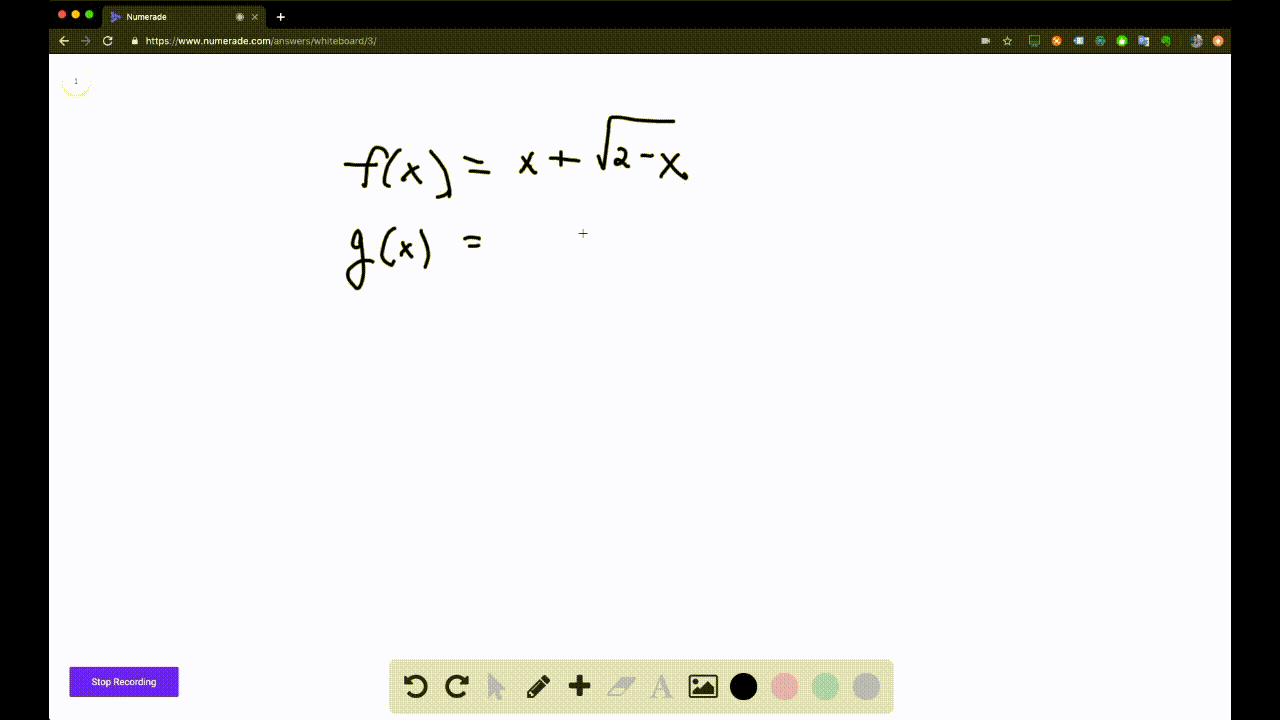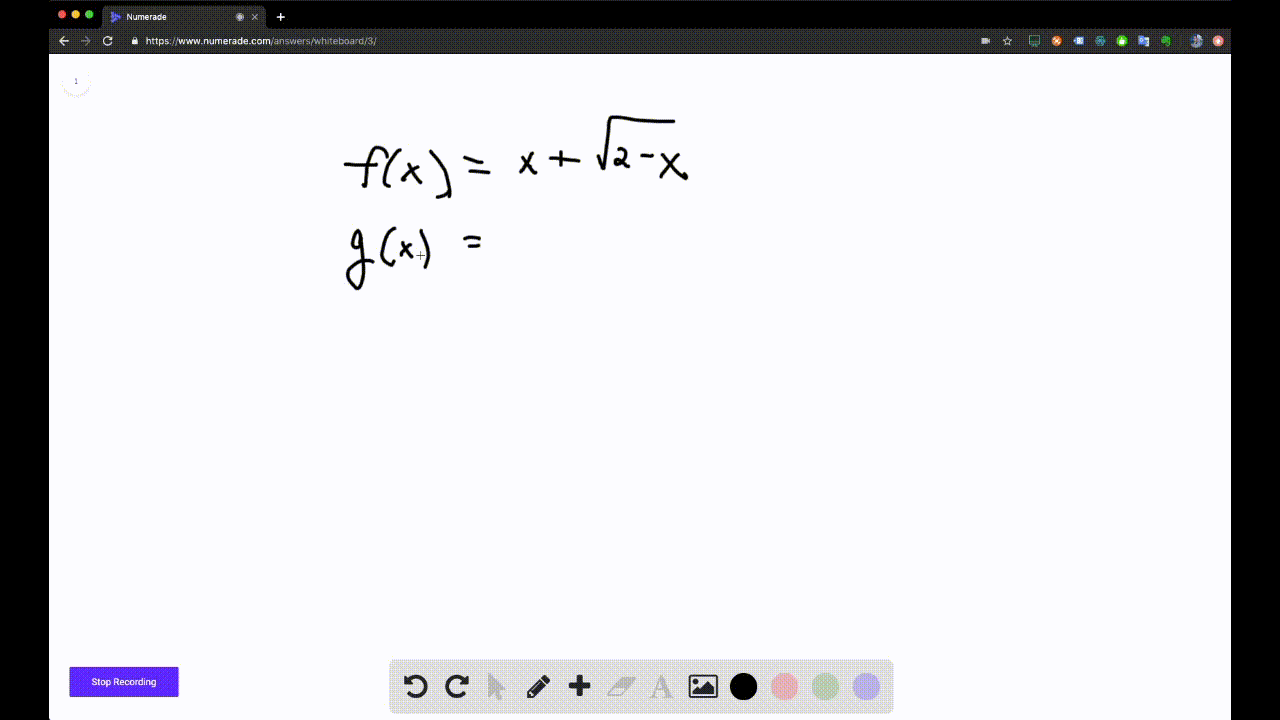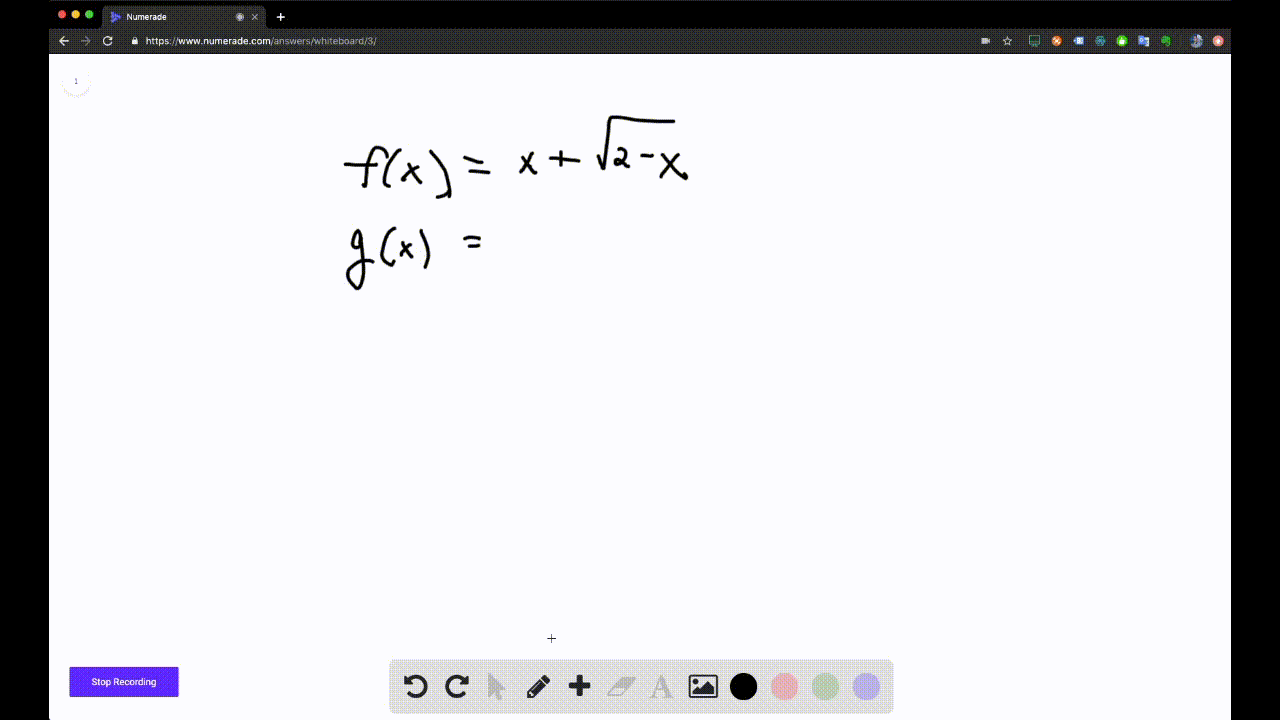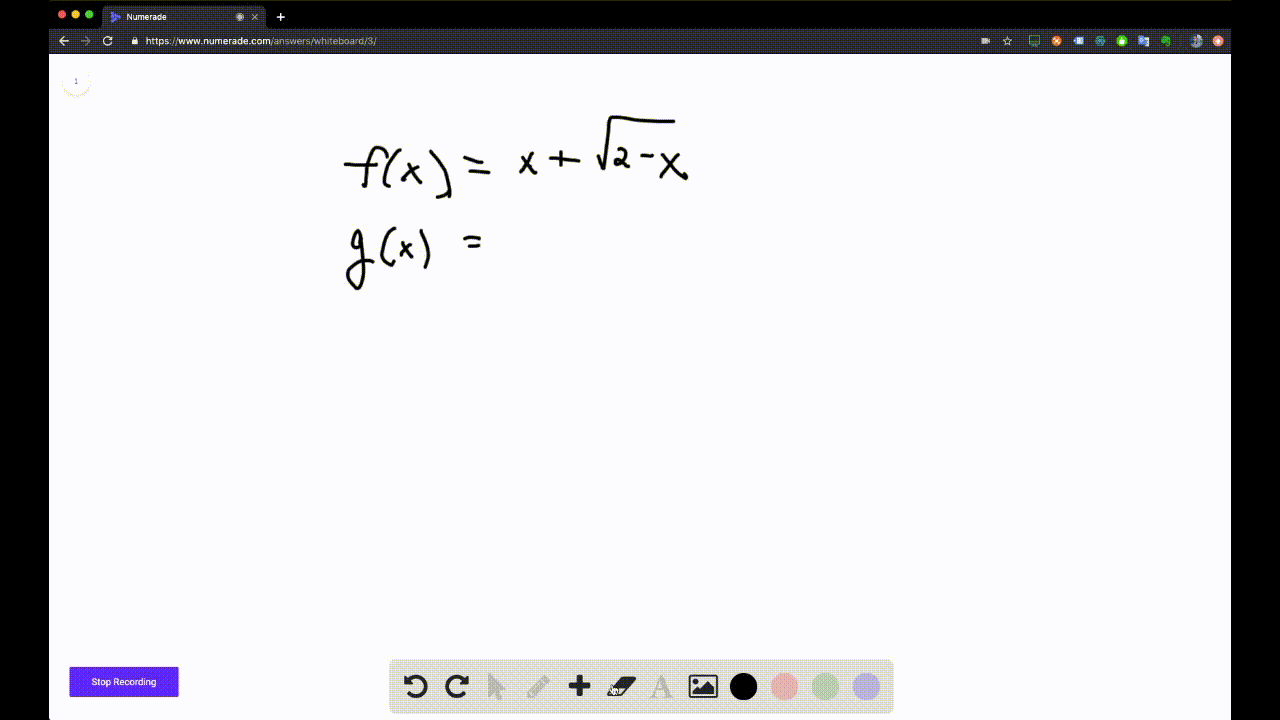



Solved If F X X Sqrt 2 X And G U U Sqrt 2 U Is It True That F G
The Derivative tells us the slope of a function at any point There are rules we can follow to find many derivatives For example The slope of a constant value (like 3) is always 0;The domain of g o f is the set of all values of x so that aSee all Words by Length at More Words Find that difficult long word here!




Home Florida Global University Bachelor Programs And Masters




Integral Calculus Formula Sheet 0
ALPHABETICAL INDEX (A B C D E F G H I J L M N O P R S T U V W Y) (Revised 06/05) A Absences Without Pay (DockF=6 G= 7 H= 8 I=9 J=10 K=11 L=12 M=13 N=14 O=15 P=16 Q=17 R=18 S=19 T= U=21 V=22 W=23 X=24 Y=25 Z=26 Classroom Activity 2 Math 113 The Dating Game Introduction Disclaimer Although this is called the "Dating Game", it is merely intended to help the student gain understanding of the concept of Standard Deviation It is not intended toWhich is the product rule Similarly if f= u=v, then d(u=v) dt = f u du dt f v dv dt = 1 v u0 u v 2 v0 = u0v v0u v;




Universal Knee Type Milling Machine Fgu 32 Tos Olomouc S R O




Scaling Functions Horizontally Examples Video Khan Academy
→ ∇g(−2,1,1) = (2e,−4e,−4e), →u = 1 √ 14 (1,−2,3), therefore D→ u g(−2,1,1) = → ∇g(−2,1,1)→u = − e √ 14 7 6 Let f and gbe two differentiable real valued functions of a single variable Show that any functionWhere g(u,v) is obtained from f(x,y) by substitution, using the equations (3) We will derive the formula (5) for the new area element in the next section;




Display Of The Scatter Plot Ground Truth Vs Prediction Of The Four Download Scientific Diagram



Fg University On The App Store




Worked Example Chain Rule With Table Video Khan Academy




Ayala Life Fgu Center Office In Cebu City




Fgu Nord Home Facebook




Complementary Literal An Overview Sciencedirect Topics




Solved If F X X Sqrt 2 X And G U U Sqrt 2 U Is It True That F G




Solved 3u 8 B Given That G U 4 Function Rule For G 1 Chegg Com




Father We Commit To You Chords Top Christian Lyrics



2




Franco German University




Ayala Life Fgu Center Alabang Tectonium



Fg University Apps On Google Play




Fantasy Grounds Unity



2




Integration By Substitution




If F And G Are The Functions Whose Graphs Are Shown Let U X F G X V X G F X And W X G G X Find Each Derivative Wyzant Ask An Expert




Q11 If F 3 G U And U U X Then A F X 9 U B F X 9 U C F A U X D None Of These




Let A A B C D E F B C D E G And C B C F G Be Subsets Of The Set U A B C D E F G H Draw Venn Diagrams To Represent The Following Sets I A Cap B Ii A Cup ap C Iii A B




Fantasy Grounds
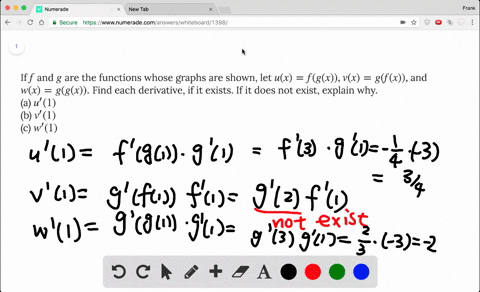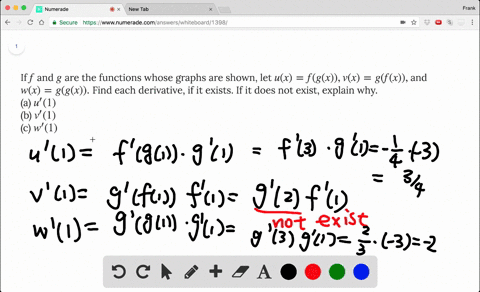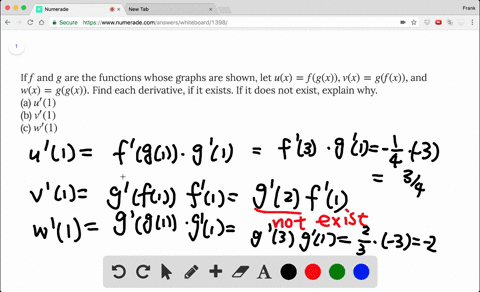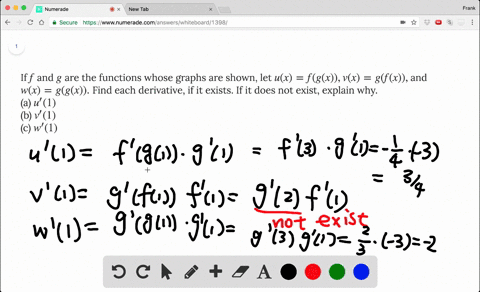



Solved If F And G Are The Functions Whose Graphs Are Shown Let U X F G X V X G F X And W X G G X Find Each Derivative If It Exists If It Does Not




Then F Is Riemann Integrable
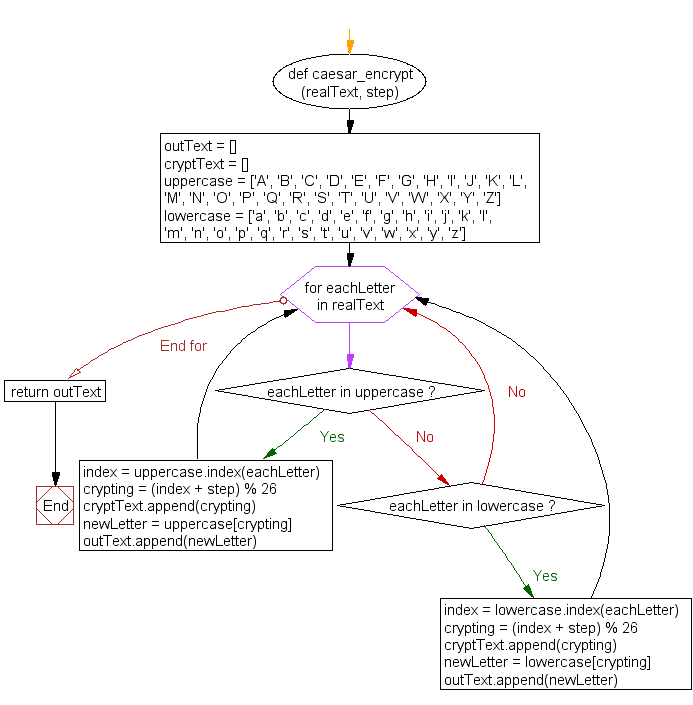



Python Create A Caesar Encryption W3resource




Solved Find F G F G Fg And F G And Their Domains F X Chegg Com




Fgu lborg Fguaalborg




Fgu Images And Layers Demo Titles Youtube



2




Home Florida Global University Bachelor Programs And Masters




Fantasygamesunlimited




Solved Let F G And H Be Functions Of Two Variables That Chegg Com




If U A B C D E F G H Find The Complements Of The Following Sets I A Youtube




Fantasygamesunlimited




The Road To Dis Battlemap Jpg Oc Fgu Fvtt Battlemaps




Scientific Machine Learning With Julia The Sciml Ecosystem




Pfrpg2 Fg Unity Themes



2



Fantasy Grounds Unity Vs Roll Why Fgu Is Better Dnd Exchange




Fgu Hovedstaden Overview Competitors And Employees Apollo Io




U F G Leq U F U G Proof Upper Riemann Integral Mathematics Stack Exchange



2




How To Change Wifi Password Step By Step Process For How To Reset Wifi Password Whatidea1




Solved Let F G And H Be Functions Of Two Variables That Chegg Com




Temple Of Sune Battlemap Animated Jpg Mp4 Oc Fgu Fvtt Allthingsdnd




Chord Veil Fire Force 炎炎ノ消防隊 Ending Theme Keina Suda Tab Song Lyric Sheet Guitar Ukulele Chords Vip




Fazo Fg U Notice Lyrics Genius Lyrics




Solved Given The Following Functions F U U 7 2 And G X Chegg Com




Solved If F X X Sqrt 2 X And G U U Sqrt 2 U Is It True That F G



2




Ayala Life Fgu Center Makati 1066 Emporis




Solution Universal Set U A B C D E F G H 7 8 9 A B 7 D G H B A D F G 7 9 C E G 7 H A Represent Infor On A Venn Diagram



3 3 Differentiation Of Compositions Of Functions The Chain Rule




Chinese Language Instruction Center Of The Office Of International And Cross Strait Affairs Fgu



2




Black Je U Explicit By Fg St 51 On Amazon Music Amazon Com
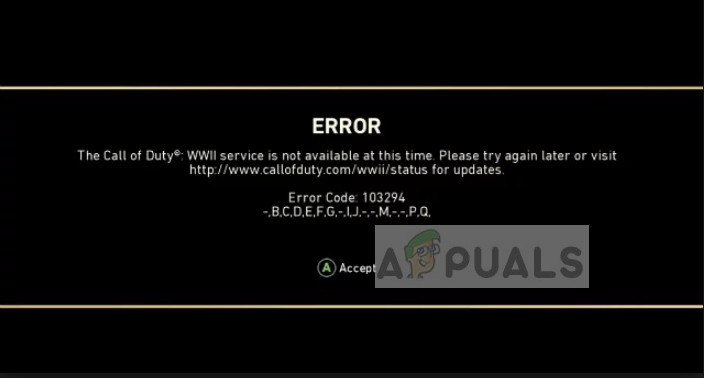



Fix Cod Ww2 Error Code Appuals Com




Fgu Nordvest Euc Nordvest




If Y F U Is Differentiable Function Of U And U G X Is A Differentiable Function Of X Then Proven That Y F G X Is A Differentiable Function Of X And Dy Dx Dy Du Xx Du Dx




Ayala Life Fgu Center Makati 1066 Emporis




Velkommen Til Fgu Syd Og Midtfyn




Gu Lock Gu Multipoint Lock Atrium Locks Ferco Atriumparts Com



Iterative Pixelwise Approach Applied To Computer Generated Holograms And Diffractive Optical Elements




Bpi Philam Alabang Formerly Ayala Life Fgu




Ayala Life Fgu Center Ayala Avenue Makati Tectonium




Children Alphabet Animals Letters B C Stock Vector Royalty Free




Emerald Cut Diamond Eternity Ring U Setting Emerald Cut Eternity Ring Kingofjewelry Com



2




Solved 1 Express The Function In The Form F O G Use Chegg Com




Fgu Emu Danmarks Laeringsportal Youtube
コメント
コメントを投稿